Here is the Knol referenced above, with my comments in [square brackets]. Everything not in square brackets is verbatim quotation. If you have any background in math, hopefully if you don’t, feel free to follow along:
The short answer to the above [Are the real numbers well defined] question is no. [OK, stating a “fact” with nothing to back it up.]
Why? Although all numbers are well-defined up to and including the rational numbers, the irrational numbers have never been well-defined. [Restating the same “fact” again, as evidence?.]What does it mean to talk about anything being well-defined? An object or a noun that has clearly distinguishable limits or boundaries is well-defined. [I thought it was something that has a rigorous definition.]
In the theory of real analysis, real numbers are defined as limits of equivalent convergent sequences (a.k.a Cauchy sequences). [Not exactly. The are several definitions, but the closest one to what he describes is “real numbers of equivalence classes of Cauchy sequences”. The AKA is certainly not true — over many metric spaces, there are Cauchy sequences that do not converge.] Herein [in the incorrect statement of what the real numbers are defined as] lies the core problem with the modern theory of real numbers [or rather, with the theory as stated by John Gabriel]: it is impossible to know the limit or boundary of any irrational number given a convergent sequence that represents the same.[Irrational numbers do not have a “limit” — they are numbers, not sequences. If we do use the ‘Cauchy sequences of rationals’ definition for real numbers, irrational numbers would be the equivalence classes containing non-convergent sequences (it’s an easy lemma to see that an equivalence class either all converges or all diverges) But regardless of the specific definition, irrational numbers do not have a “limit” or “boundary”, as they are numbers. Whether we can know stuff about them is irrelevant to their definition. “All Cauchy sequences up to the equivalence relationship defined as ‘the difference converges to zero” is a definition of the real numbers which is as clear cut as any.]
So how then, is it sensible to claim that such a definition is well-defined? [By not giving a strawman definition, I guess.] It fails in the very first requirement to match the attribute for being well-defined, that is, its limit or boundary is unknown. [The strawman definition fails in that it begs the question: if irrational numbers are, indeed, limits, then they would have to be defined before they are used. I guess that this is a roundup way of going about that.] For example, consider the well-known irrational number called pi. [That “irrational number” can be represented as a real number easily enough: one example is through the Taylor expansion for arc-tan, and taking the arc-tan of something we can construct Pi from via additions and multiplications with rationals.] Although we can calculate the approximate representation of pi in a radix system to almost any degree of accuracy [In other word, for any real number, there is a unique Cachy sequence in its equivalence class such that a_n is b_n/10^n with b_n being natural, and such that the sequence is not eventually constant.], it is incorrect to state that we know the limit of a convergent sequence that represents pi. [No it isn’t. After defining the real numbers as such Cauchy sequences, we can identify the rationals with the equivalence class of constant sequences. It is then trivial to prove that if r is a real number, and q_n is a member of it, then q_n seen as a Cauchy sequence of real numbers converges to r. It is subtle to understand that we identify two different representation of the rational numbers: one as the regular ol’ rationals, and one as the subset of the real numbers. However, in general, any two structures isomorphic up to a unique isomorphism can be identified is a usual thing, and brings no ill effect. A different way of saying it is “the rationals are the smallest field of characteristic 0”, and take any field satisfying that as the field of rationals.] To say that 3.1415926 as a value for pi is accurate to seven decimal places means nothing. [Ummm….it needs to be well-defined, which is not to say it means nothing. Here’s a stab at a definition: a finite decimal expansion is accurate to n digits if it differs from the number it represents by less than 10^n.] It is only an approximation. [Yes, it is an approximation, accurate to 7 digits. What’s the problem with that?] Furthermore, this approximation is not sufficient for all calculations involving pi. [Right. If it was, it would be pi, not an approximation of pi.] Therefore it can be confidently stated that pi is not well-defined, [Umm…no, it can be confidently stated that pi is distinct from its finite expansions. At least confidently if you prove it, but the details of this proof are immaterial to his thesis, which could have used some other number.] except to say that it is a ratio of a circle’s circumference length to its diameter length. [That’s certainly one way to define pi.] The components of such a ratio are neither rational numbers [indeed, though not trivial to prove], nor limits of sequences composed of rational numbers that supposedly represent these irrational numbers [Ummm…yes, they are. I just constructed such a sequence above in my definition of pi, and it converges to pi by the lemma I alluded to earlier.] . Reason? Such limits are indeterminate. [No, such limits are determinate. Here is a sketch of the proof: assume r is a real number, and q_n is a member of it. Let p_n be another member of it. By Cauchy propery and equivalence, for a given epsilon, for sufficiently large m, n, q_m-p_n will be less than epsilon. Therefore, q_m-r will be less than epsilon. The details are beyond the scope of this text, but are not hard to fill in.]
[I’m skipping over some discussion of a flaw in Cauchy’s argument. I don’t know enough history, perhaps Cauchy’s arguments were wrong. That does not matter. The definitions still work. Above I alluded to proofs that work. You can pick up any advanced calc. book and get the details, and the proofs there work — I did check the proofs in my copy. That’s the nice thing about math — even if Cauchy was wrong, it doesn’t impact any of modern math. Calling the sequences Cauchy as an honor is still appropriate — he showed the way, even if he got stuff wrong. Real mathematicians are happy to fix the problems and move on.]
An irrational number exists as a magnitude in reality but does not exist in theory. [Here we veer off math into philosophy. For all I know, this guy’s philosophy is sound. His math, in any case, isn’t. What does “exist” mean in this context? For me, “the real numbers exist” is a theorem in ZFC which states “there exists a complete ordered field”. I can prove this theory, and every decent calc book proves this by constructing the real numbers. There are many different constructions. Some of the easiest use Choice, but it’s not endemic — there’s a famous construction from almost-homomorphism which uses only ZF. See wikipedia for more details. Whether it exists in “reality” or “theory” is a different question entirely. It is possible that ZF is inconsistent, and thus proves everything including the existence of real numbers in uninteresting ways.] For example, in an isosceles right-angled triangle whose equal sides are joined by a theoretically immeasurable [what does “theoretically immeasurable” mean?] quantity called a hypotenuse, the length of the hypotenuse is real in every respect. [Things can be real in more than one respect? Clearly, this is pure philosophy.] It can be formed from one of the equal sides and part of the other equal side. The part of the other equal side can be constructed to complete the length of the hypotenuse:
[A drawing follows]
Now it is easy to see how an irrational ‘line segment’ exists in practice. Theoretically, an irrational number cannot be defined (neither as a Cauchy sequence, nor in any other way). [I have no idea what he means by “theory” or “practice”. Mathematically, irrational numbers can be defined. I just gave a definition above: equivalence classes of Cauchy sequences that do not converge.]
The successor of zero is an indeterminate quantity (not an infinitesimal because an infinitesimal is an ill-defined concept) [As opposed to an indeterminate quantitiy, which is a well-defined quantity? I’ve never seen a definition for that, and certainly not in this text. In any case, an infinitesimal can be well defined (a member of a an ordered field that contains R which is smaller than every positive real), and is irrelevant as it is still not “the sucessor of zero” which I have no idea what he means by. Infinitesimals in classical non-standard analysis are still members of a field, so the “smallest infinitesimal” still does not exist — if p is infinitesimal, so is p/2.] that arises in the measure of all irrational numbers because it cannot be represented as a/b. [It does not arise in the measure of all irrational numbers, even though they can be represented by a/b. His conclusion fails to follow from the premises. It, in fact, fails to be clear enough for me to understand…] So when one tries to measure any irrational number [what does “trying to measure an irrational number” mean?] using sums of averages (a Cauchy sequence for example) [How is a Cauchy sequence a sum of averages?], there is no such thing as ‘limit’. [Cauchy sequences over the real numbers always have a limit.] It does not matter that a value for the limit can be fixed for any given partial sum as in the epsilon-delta arguments. Why? [Why, indeed!] Provided more terms are summed in a partial sum, the limit continues to change even though it (limit) converges [I don’t understand. The limit is a number. It does not converge to anything. The sequence converges to the limit.] (To what? No one knows for certain…the limit cannot be a number because a number is defined as a ratio!) [What! The! Hell! Where was a number defined as a ratio? He pulled this out of his hat in the middle of the discussion. I assume he means “an integral ratio”. Well, if that’s his definition of a number, clearly the real numbers are not numbers. But it’s just using a different definition. Fine, call a complete ordered field the real “lumbers”. Now every Cauchy sequence over the rationals is a lumber. Real numbers are well defined — they just differ from his definitions. While theorems are a matter of truth, definitions are a matter of convenience and thus convention. Flauting convention is just not useful here. Is the point maybe to say “I want to have an unorthodox definition of numbers”? Because I could say that too. A number is 5. 5 is the only number. This definition is just as good as his — equally unpopular, unhelpful and yet valid.]. The successor of zero [which he didn’t define] is the reason a limit does not exist for any irrational number. [An irrational number has no limit because it’s a number. Sequences have limits. Numbers…are just numbers.]



http://xkcd.com/406/
I read the original knol you refer to. I do not recall him mentioning anything about a real number having a limit. He writes about limits in the correct sense, i.e. the upper bound of a Cauchy sequence. Could you tell me where he writes this please?
You write there are Cauchy sequences that do not converge in Metric spaces. This is false. All Cauchy sequences are convergent. It is a requirement for a sequence to be convergent so one can call it Cauchy, no?
Moshe, I had to stop reading your article because it is full of errors. Please fix it before you criticize others.
* “it is impossible to know the limit or boundary of any irrational number” (quoted from the knol). Just because you don’t recall it, doesn’t mean it doesn’t exist.
* Limits are not “the upper bounds of Cauchy sequences”, the upper bound of a Cauchy sequence is irrelevant. Not that he mentions upper bounds anywhere, but your statement is incorrect.
* The Cauchy sequence “(1+1/n)^n” over the rationals does not converge. The Cauchy sequence “1+p+p^2+….” does not converge over the rationals with the p-adic metrics. It is true that every metric space could be embedded in a metric space in which all Cauchy sequences converge. However, the proof for that includes dealing with non-convergent Cauchy sequences.
Your criticism is meaningless, but hey, thanks for taking the time to come into my blog and spout three non-sensical statements, and then cautioning me not to “criticise others” (what the frell? I thought peer-review is a part of math. If you disagree, state your disagreements, but don’t threaten reprisals…)
“Moshe, I had to stop reading your article because it is full of errors.”
Hehe. You obviously don’t know Moshe.
“It is a requirement for a sequence to be convergent so one can call it Cauchy, no?”
The short answer is, indeed, “no”. Or else we would be calling them “convergent sequences”, not Cauchy (why invent a name for something so simple?). Every Cauchy sequence converges in a complete metric spaces (e.g., the reals), but certainly not in an arbitrary metric space. Here is a good source:
http://en.wikipedia.org/wiki/Cauchy_sequence
Unlike knol, wikipedia is reasonably trustworthy.
You know, it is not very wise to make strong statements such as “You write there are Cauchy sequences that do not converge in Metric spaces. This is false.” before checking the basic definitions (which are very easy to check).
You are quoting me out of context. You normally do this, don’t you?
Limit of a number: Every real number is defined in terms of equivalence classes of rationals in real analysis. Although the limit is the idea of real number, I use the phrase to indicate that whatever real number is being considered, it is impossible to know its extent, unless it can be finitely represented.
You talk about Cauchy sequences not converging over the rationals. I was decribing C. sequences converging over the reals. Every Cauchy sequence is convergent over the reals. Your mention of metric spaces is irrelevant – the reals are a complete metric space.
No one should trust anything they rad on the internet – especially your site from the look of things!
Quoting you out of context? It would be nice if you had some context.
* Ummmm…ok, once again, you fail to give the accurate description of real numbers. Real numbers are defined as equivalence classes of Cauchy sequences of rational numbers, not “equivalence classes of rational numbers”. Is that again out of context?
* There’s no “ideal” of a real number. I have no idea what you mean by “extent” of a real number. In fact, I have no idea what you mean by “know”. I trust you’re not talking about knowing real numbers in the carnal sense, but barring that definition, I really have no idea what you’re referring to.
* You were describing *C*? How is anyone to know that, reading your knol, given that you don’t even mention the complex numbers?
* Of course every Cauchy sequence converges over the real numbers. But I think you said “the real numbers are not well-defined” (I guess this is again quoting you out of context?) The classical construction of the real numbers from rational Cauchy sequences by necessity has no convergence — the real numbers haven’t been defined when the rational Cauchy sequences are introduced.
To whit, here’s the point summarized: you claim the real numbers are not well-defined. You give confused arguments to that effect, including some that *assume the real numbers are well-defined*.
The standard way I learned to think of the real numbers is as followed:
* Define a complete ordered field
* Prove that every two complete ordered fields are isomorphic up to a unique isomorphism
* Use any of the constructions (Cauchy sequences, Dedekind cuts or some of the more esoteric ones) to prove that the real numbers exist.
I’m not sure which of these steps you have a problem with, though I suspect it’s the last. However, you have not managed to point to any flaws in the Cauchy sequence constructions. Mind you, the Cauchy sequence construction is really tagential to the whole discussion — there are many other constructions, some of them having nothing to do with limits (see the construction using almost-homomorphisms from Z to Z), and none of them requiring us to “know” real numbers to any “extent”.
Moshe, he doesn’t mean that he is describing C = the complex numbers. He means “C. sequences” (that is, Cauchy sequences) over the reals. Which are indeed convergent. I don’t see the relevance of this to your discussion, but that’s a different issue.
What Moshe is saying is that there is absolutely no mathematical inconsistency in the construction of reals. And he is right.
If I understand your objection correctly, it is meta-mathematical rather than mathematical. You don’t believe in infinitary objects. That is, the real numbers can be seen as (identified with) infinite sequences of natural numbers (or rational numbers), and you only believe in objects (e.g. numbers) which have finite descriptions. That is a valid philosophical point of view, but it says nothing about the validity of a certain mathematical proof.
The mathematical proof of existence of real numbers is correct, but it relies on certain axioms of set theory, such as the axiom of infinity and the power set axiom, which one might not believe in. In fact, taking a step back, there is even no “proof” of the existence of the set of all natural numbers, unless one takes the axiom of infinity on faith. And as we know by the Incompleteness Theorems, this “belief” is essential: we will never be able to prove that the natural numbers (as a set) exist, unless we work in a stronger framework of axioms, which we have to take on faith. The only thing that might happen is that one day somebody will discover inconsistency in Peano Arithmetic; but nobody will ever be able to prove its consistency without relying on something that itself can not be proven using only finitary objects. So the only sets that we know for sure exist are finite. That is, we know that every natural number exists separately, but putting them together into an infinite set requires belief.
One may also believe in the existence of natural (hence rational) numbers, but the power set axiom applied to the natural numbers is yet another major step, and one can decide it is too much for them to take on faith. In that case, in your framework there indeed will not be a proof for the existence of the reals.
But since we, as mathematicians, believe in the set theory axioms of Zermelo-Fraenkel, the proof of the existence of the real numbers is just a simple formal application of those. And there is no problem with it.
Having said all this, I have to add that your response to Moshe didn’t make much sense. You are arguing about mathematical issues, so you have to be much more precise and rigorous in your statements. For example: yes, Cauchy sequences converge over the reals, but weren’t you claiming in your article that reals are not well defined? So how can you talk about Cauchy sequences over objects which are not well-defined? Moshe’s criticism of the mathematical aspects of your article is in place, and you will have to address it, if you want people to take what you are saying seriously.
What do you mean by “finitely represented”? For example, are computable real numbers finitely represented in your book? There is a finite algorithm that “represents” them. What about real numbers that people call “measurable” (nothing to do with measure theory, this is a somewhat vague notion introduced by physicists of numbers that “occur in nature”, that is, can be measured by an observer)?
Indeed, you have quoted me out of context. If I say “equivalence classes of rationals”, it is because I assumed that you (who *claims* to be a mathematician) would understand from the context, that this means *equivalence classes of convergent sequences*. Now do I need to say *convergent sequences of rationals* also? No, it follows once again from context.
Yes, I claimed the real numbers are not well-defined because they are not. I am not going to explain this to you here. I wrote a knol which describes my thoughts on this topic (The knol is called “Are the real numbers well-defined?”). If you had bothered to read it, you would not be as arrogant as you are on this site. Frankly, I am doubtful you have the intelligence required. Or perhaps your prejudice simply overrides all common reason so that you are incapable of thinking for yourself.
It is not true that equivalence classes of convergent sequences define the real numbers. What is this “limit” (of a convergent sequence..) you are referring to? Is it a number? If yes, what kind of a number is it? My knol answers these and other questions in detail.
You are faithfully regurgitating the nonsense you were taught in a real analysis course if indeed you completed one. I have completed courses in advanced mathematics and two of these courses were Analysis of Reals (or Basic Analysis) and The theory of Metric Spaces. I am not going to discuss this theory with you because much of it is incorrect.
Finally, I am not very amused when you call me confused and it is actually you who is confused.
I am not intellectually inferior to you, so spare your disdainful comments for someone who is closer to your level.
Alex: Thanks, but I don’t need you telling me what Moshe is trying to say.
* Clearly, you and I mean different things with the word “context”. Yes, I am a mathematician. I am led to believe that (a) you write only for mathematicians who are able to understand your context and (b) so far I’m counting three mathematicians who failed to understand your context. May I suggest actually writing in the details? While sometimes it is ok to leave easily understood details out, putting them in is a sure-fire way to prevent misunderstanding. In any case, it certainly makes it hard to refute the arguments, as well as understand them in the first place, if you keep using words contrary to accepted meanings.
* I read the knol to which you are referring. I even gave a link at the beginning of my post, for interested readers — as well as quoting it, at length, explaining my specific issues with the claims made in it. In fact, that is the context of my blog post.
* Ad-hominem attacks are really beneath me to respond to. I’ll just mention a few of the ones you make in the post above, to clarify what I mean: “I am doubtful you have the intelligence”, “you are incapable of thinking for yourself”, “you are faithfully regurgitating the nonsense you were taught”, “I have completed courses in advanced math”, “spare your disdainful comments for someone who is closer to your levels”. I don’t think that we need to drag credentials into a debate about math — math doesn’t care about credentials either way.
* I never said that equivalence classes of convergent sequences define the real numbers. I said that equivalence classes of Cauchy sequences are (one possible) definition of the real numbers. You are misquoting me there. [Not quoting me out of context — literally putting words in my mouth I have never said]
* I did not call you confused, contrary to what you said. I said that your argument was confused. It was — it was not a coherent mathematical argument.
* I am not sure what you mean by “incorrect theory” in the math sense. In physics, theories can be incorrect (for example, Newtonian mechanics is incorrect as it gives wrong results when the speed is close to the speed of light). However, in math, theories are not measured by the physical world. I understand what it means for a theory to be “consistent” (and the theory of real numbers, namely the existence of a complete ordered field) is “at least as consistent of ZFC” (see Alex’s remarks above regarding needing qualification of claims of consistency). I have sketched out a proof, as well as pointed to the Wikipedia article about construction of the real numbers.
So, in summary, your comment above has:
* A weird new math, wherein context means “whatever it is I neglected to mention but retroactively put in”
* Ad hominem attacks
* Misquotations of my arguments.
I am giving you the benefit of the doubt, and assume none of this is done with malice. In this spirit, let me suggest some guidelines for reasonable debate:
* I can only criticise what you write, not what you mean, as I lack telepathic powers. However, I am more than happy to see an amended argument, and I will be happy to retract any criticism that no longer applies. If there’s a version of the argument in the knol that is more rigorous, please point me at it.
* Please refrain from attacking the person doing the criticism, and make your counter-argument by criticising the argument itself. I have not called you names, and I expect the same level of civilized discussion from you.
* Please avoid misquoting me. Please make sure that I said the exact words you say I said. I assume your browser has a search button, and I encourage you to use it.
John: actually, I wasn’t. I was just trying to interpret what you are trying to say. Please read my comment carefully and take it seriously, as have I with your comments.
You may claim that all the answers are contained in your knol article(s). But they are not. As you have pointed out yourself in this discussion, there is too much in your articles, which is supposed to “follow from the context”. I have seen too many actual mistakes in mathematical papers (including first drafts of my own papers!) which came precisely from the fact that the author (in certain cases, me) assumed that something was clear from the context, when in fact not only was it not clear, but there was an important subtle issue hidden in that (wrong) assumption.
Since you are not commenting on my questions, let me be very precise. I would like to ask you what is wrong with the following (classical) definition of real numbers. And I would appreciate a precise and specific answer.
I assume you are familiar with the classical construction of a completion of a metric space. Still, let me briefly go over it, in the very particular case of the rational numbers.
I will be working in set theory, assuming all the axioms of Zefmelo-Fraenkel. I am given the set of rational numbers Q, and I will define the set of real numbers R.
First, let B be the set of all Cauchy sequences of rational numbers.
Note: Cauchy, not convergent. You are saying in one of your responses to Moshe: “… would understand from the context, that this means *equivalence classes of convergent sequences*. Now do I need to say *convergent sequences of rationals* also? No, it follows once again from context.” See, you are making a mistake here. If you take sequences which actually converge in Q, you will not be adding anything new. Most Cauchy sequences do not converge in the rational metric space. If you mean “convergent in R”, this doesn’t make sense, because R has not been defined yet. You would get a circular definition of R, assuming the existence of R. If this is what you actually had in mind, I would agree with you – this is not a good definition.
Let me continue. So B is the set of all Cauchy sequences on Q. Define the equivalence relation E on those sequences saying the they eventually “come arbitrarily close”. That is, given two Cauchy sequences [a], [b], they are E-equivalent if for every epsilon>0, there are N,M such that if n>N,m>M, we have that |a_n-b_m|<epsilon. There are different ways of defining this relation, but it doesn't matter.
First, you prove that E is an equivalence relation on the set B. This is easy. Hence there exists the set R of all equivalence classes of B modulo E, R = B/E. This is a standard set-theoretic argument, that does not require almost anything. We have obtained a set, which we call the set of real numbers.
This gives a good definition of real numbers. Since every step in the construction above is mathematically sound, you can not claim that this particular set R (which is what is called in mathematics the set of real numbers) is not well-defined. Because the definition is right there.
One objection you might have is to some of the axioms of set theory that were used in order to claim, for example, that the set B exists. Not believing in those axioms would be a valid meta-mathematical point, because, as we know, there is no way to prove that the set of axioms of set theory is consistent. And this is what I was saying in my previous comment. But since you have not replied to that comment, I assume that this is not the problem that you have, and I am still trying to understand what is.
I have given you above a sound mathematical proof of the existence of the set of real numbers. That is, I have shown you that (assuming certain set-theoretic axioms) this set is well-defined. My question to you is: what is wrong (according to you) with my argument? Are you claiming that there is a problem with this proof? Or do you not believe in one of the set theoretic axioms required for the proof? Since (I hope) we agree on the concept of mathematical proof, these are the only two options for you not believing that what I have described is a good definition. But possibly you do not think that this definition describes what people (non-mathematicians) refer to as real numbers?
[Moshe: cleaned up HTML. Did not touch any of the content.]
Great. I think there is some HTML code that was hidden in my comment. I can not edit comments, but I think Moshe can fix this manually.
[Moshe: Done.]
Your response was what I expected – lacking in any real substance. The arguments you called *confusing* are clearly addressed in the Knol. This is the reason I suggested you read it carefully. All the so-called *objections* you raised are addressed.
You claim ad-hominem attacks are beneath you, yet what exactly are your *objections*?
You have a very short memory, so I shall remind you:
“Real mathematicians are happy to fix the problems and move on”
“What! The! Hell! Where was a number defined as a ratio?”
Sufficient or do I need to mention more? Look, if you want me to address particular objections, state these and I shall address them one at a time. You shall find that a lot of the others are answered once you understand the first few answers.
Let’s begin with the first objection: Are the real numbers well-defined in several ways. No. A Cauchy sequence fails to defined a real number. Also, a Dedekind cut fails to define a real number.
Why does a Cauchy equivalence class fail to define a real number? Answer: A limit is an ethereal concept that is defined in terms of itself. Any irrational number cannot be represented except by approximation.
What is the limit of pi? Is it a number? And yes, a number is by default a ratio of two magnitudes. What is a magnitude? A magnitude is the idea of size or extent. All this and much more is described in my Knols. It actually pays to read them all.
My Knol called “What is calculus all about?” contains links to other Knols I have written. Read all of these Knols and the concepts shall become clear.
I’ll ignore all your rhetoric, as you seem to request, and concentrate on the math —
“Why does a Cauchy equivalence class fail to define a real number? Answer: A limit is an ethereal concept that is defined in terms of itself.”
I have no idea what you mean by that.
* An equivalence class of Cauchy sequences (I assume that’s what you mean by “Cauchy equivalence class”, but it would really help the discussion if we try to stick to the accurate terminology rather than shorthands) is defined without a reference to a limit. You can see Alex’s definition above, or check any calculus text. Alex’s definition is equivalent to the one in http://en.wikipedia.org/wiki/Construction_of_the_real_numbers#Construction_from_Cauchy_sequences in case you want a neutral third party verification. Let me quote from wikipedia: “Two Cauchy sequences are called equivalent if and only if for every rational ε > 0, there exists an integer N such that |xn -yn| N.”. There is no reference to a limit here, so I’m not sure what your complaint refers to.
* A limit is not an ethereal concept defined “in terms of itself”. It is accurately defined in any number of calculus text books, and again I’d refer you to wikipedia: http://en.wikipedia.org/wiki/Limit_of_a_sequence#Formal_definition and I quote ” A real number L is said to be the limit of the sequence xn, […] if and only if for every real number ε > 0, there exists a natural number N such that for every n > N we have |xn−L| < ε." (I removed the way to write it, but other than that my quotation is accurate). In fact, it is possible to define the equivalence of Cauchy sequences in terms of limits: "x and y are equivalent if x-y has 0 as a limit". It is an exercise given to first year students to verify that these definitions are, indeed, the same. So in case it so happened that you saw a definition of the equivalence in terms of limits, it is *still* a valid definition.
"Any irrational number cannot be represented except by approximation.
What is the limit of pi? Is it a number? And yes, a number is by default a ratio of two magnitudes. What is a magnitude? A magnitude is the idea of size or extent"
I'm not even sure how to reply to this. This is exactly what I call a "confused" argument. It gives several terms, does not define them formally, and proceeds to ask questions about them which are impossible to answer, given the lack of clear definition — and then draws the conclusion that irrational numbers are not "well-defined" (I'm not sure what you mean by that.)
Terms which are not defined in the segment above:
* "represented" — what do you mean by "representing" a number? Do you mean by marks on paper? Alex gave you above a way to represent pi using marks on paper: write out the definition of a turing machine that prints out pi. Using such an approach, you'd get the "constructive reals", which are not the same thing as real numbers, but many of the theorems can be converted appropriately ("any constructive set of constructive reals has a constructive upper limit" given appropriate definitions of the terms). Note: I know I have not given a definition of the constructive reals. They are really tangential to my comment: that your use of "represent" as it applies to real numbers has not been defined, and that in what meanings I can give it, what you said is not true. Thus, if I am to understand what you wrote here, you'd need to give a definition. I've gone over half a dozen of your knols and have failed to find such a definition. Maybe I am missing something, but a more specific reference than "I wrote a knol" would be appreciated. See the references above: I gave a link, and quoted. If you could do the same, and point to a definition of "representing" numbers, it would be possible to understand what you're saying.
* "A number is by default a ratio of two magnitudes": OK, so all I see here is that you are giving a different definition of a "number" than anything I have ever seen. In math, definitions are a matter of convenience: nobody ever *has* to talk about real numbers (we could just talk about complete ordered fields). As such, we choose such definitions as have been convinient throughout history, and as such the definitions are a matter of historical accident, not mathematical content. I would greatly appreciate if you stuck to the common definition, otherwise you are throwing unneeded hurdles onto the path of understanding. In any case, if your knol is "I want to define numbers differently", and it was called that, I would not even attempt to argue with you: choosing different definitions for terms is fine as long as it is clear and unambiguous (in one of my own papers, I suggest a different definition for a popular term, so I certainly see the value in that).
* "by default": I don't understand that. Either all numbers are ratios of magnitudes, or they're not all ratios of magnitudes. What does "by default" mean in this context? Do you mean this is the default definition? It's certainly not, seeing as how most mathematicians do not use that definition. Perhaps you mean something else by "default", but again, I'm not sure what.
* "A magnitude is the idea of size or extent": this is not a definition I can understand. What set of axioms are you starting with? If you are starting with Euclid's axioms, than we have no argument: I agree that the real numbers cannot be defined using only Euclid, and need a richer basis. If you are trying to prove something like "Consistency of Euclid does not imply consistency of real numbers", well, you haven't proven that — but it's not unlikely that it's true. If you have a proof for that, that sounds like interesting. Barring that, if it's not either Euclid or ZF, then please identify the exact set of axioms you are starting with — either by name, if it's a popular set, or by enumerating them otherwise.
You claim that you have never seen my definition of number and yet you call yourself a mathematician?
A ratio of two integers is well-defined.
The definition of a Cauchy sequence does not define a real number (whatever a real number is…). It states certain properties that a sequence must have to be convergent. Your arguments are confused. Again, I ask you to tell me what is a limit? Is it a number? What is a number in your understanding? What is a limit if it is not a number?
Do not write an epsilon-delta definition for me – I already know it and understand it well. Explain to me what form the value of limit takes? Is it rational or irrational? If irrational, then what is an irrational? Again, don’t tell me an irrational is a number that cannot be written as a/b. This would be insufficient and wrong.
* I was not sure reading your definitions was a pre-requisite to being a mathematician
* The ratio of two integers is indeed well defined. Not that I’ve seen a definition in your knol, but it’s a standard construction.
* The definition of a Cauchy sequence nowhere states that the sequence be convergent. Let me reiterate the definition, and we can see it does not talk of convergence: “a sequence x is Cauchy if for every epsilon>0 there is an N such that for every m,n>N, |x_n-x_m|N such that |x_n-q|>=epsilon). A lemma that is left as an exercise to the reader is that: (a) if x in A has no rational as a limit, A is irrational and (b) If A is irrational, there are no integers n,d such that A=n/d. It’s a fun lemma to prove, since it’s mostly epsilon/2 arguments and such, and it will certainly show how real analysis is done.
Moshe, I am going to try something.
Cauchy sequences do not have to converge, as was already pointed out earlier.
Since a ratio of two integers is well defined, I assume that you agree that a Cauchy sequences of such ratios is also well defined.
Given the set B of all Cauchy sequences as above, the equivalence relation E that I defined on B in my previous comment, is also well defined.
A real number is simply an equivalence class of B modulo E. This is again well defined. So real numbers are well defined. Call the set of real numbers R.
Any problem with the definition so far?
Continuing my previous comment, I would like to say something about rational and irrational real numbers.
We saw that R is well defined, that is, R = B/E.
You can identify the rational numbers Q with a subset of R: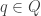 is identified with the class of the constant sequence
is identified with the class of the constant sequence  . So with this definition, the answer to your question about which elements of R are rational, and which are not is the following:
. So with this definition, the answer to your question about which elements of R are rational, and which are not is the following:
Let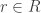 . Then $\latex r$ is an equivalence class of elements of B. If this class contains a constant sequence, then
. Then $\latex r$ is an equivalence class of elements of B. If this class contains a constant sequence, then  is called rational. If it does not contain a constant symbol, then
is called rational. If it does not contain a constant symbol, then  is called irrational.
is called irrational.
Now, it is a routine exercise to see that there is a unique way to define metric on R which extends the metric on Q such that Q is dense in R. It is also easy to see that now it is true that any Cauchy sequence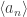 in B has a limit r in R (which is precisely the class of that sequence). Sometimes the limit will be rational (which means that the class of
in B has a limit r in R (which is precisely the class of that sequence). Sometimes the limit will be rational (which means that the class of 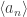 contains a constant sequence), sometime it will be irrational (which means that the class does not contain a constant sequence). But this limit is always a real number (that is, an element of R that we have defined before).
contains a constant sequence), sometime it will be irrational (which means that the class does not contain a constant sequence). But this limit is always a real number (that is, an element of R that we have defined before).
Note that I only started talking about limits in R once R was defined (in the previous comment). You are right in saying that defining “a real number is a limit of a Cauchy sequence of rational numbers” doesn’t make sense (because most of those sequences don’t have limits in Q).
Please don’t quote anything from Wikipedia to me.
Your quote refers:
“A real number L is said to be the limit of a sequence xn, …”
Let’s see what is wrong with your quote.
1) Without defining a “limit” of a sequence, you claim that some “real number” (again, no previous definition) is the limit of a sequence xn…
Problem: You are using terminology with no previous definitions. Define one or the other before you use it in a definition for the other. Start with real number or start with limit.
2) You write “..In fact it is possible to define equivalence of Cauchy sequences in terms of limits…”
Problem: Not entirely true. In fact, this is a misrepresentation. If the limits are rational numbers, then this is true. If the limits are irrational numbers, then this is not true. How do you compare irrational numbers? Answer: By the partial sums of the convergent sequence that represents those numbers. If the numbers are represented in some radix system, then this is definitely the case. In any event, this is not a full-proof method.
Otherwise, you have to show equivalence of partial sums in another way – not always possible.
3) There is no such thing as “the constructive reals” – again, a misrepresentation on your part.
Problem: The “real numbers” are inherently theoretical just as the concept of “number” is also theoretical. Our use of real numbers is based on our understanding that a real number can be approximated – how? Using sums of rational numbers.
4) You claim that nobody ever has to talk about real numbers, only complete ordered fields. You are incorrect.
Problem: You evidently do not understand basic real analysis. The requirements for a complete ordered field are: it must have no largest or smallest element and must contain partially ordered sets, in which all subsets have both a least upper bound and a greatest lower bound. This is all fair and well provided one already knows what kind of elements R has. So, for you to state that one does not require real numbers is an outright lie. It is a requirement. To put it simply: how do you arrive at any conclusion about ordering without knowing how the elements are ordered? Your arguments are not only confused, they are completely wrong.
Now, please see my previous post and tell me what you think a number is. From this concept, show me how you arrive at your understanding of real number. Yes, it is true – the reals can only be defined from a Euclidean perspective contrary to your claims.
If you go off on a rant, I shall ignore you and not visit your site again.
* Um, no, the real numbers are defined without reference to a limit, and the above is the definition of a limit. Do you expect a limit to be defined *before* it’s definition?
* It is entirely true. Limits can be defined over the rationals. In fact, if you go to the same wikipedia article I referenced, you’ll see the very next definition is an abstract definition over generic metric space.
* There is such a thing as the constructive reals. I did not give a definition above because their discussion was tangential to my argument, except to show that the concept of “represent” is ill-defined. A full definition (“a constructive real is one which has a convergent sequence of rationals q_n=a_n/b_n such that the functions n->a_n, n->b_n are general recursive functions”) is not hard to give. I’m not sure why you have a problem with it, except for your general issue with limits.
* Your definition of complete ordered field is not accurate (for example, the field as a whole has no l.u.b.). A working definition of complete ordered field is: “A field with a special subset P of positive numbers, closed under multiplication and addition and such that for every x, exactly one of x=0,x in P,-x in P is true, and that with the ordering defined by x<y when y-x in P, every bounded non-empty subset has a least upper bound". This actually works without knowing that R exists, and it can be taken as an axiom. All the construction of the real numbers gives is to show that this axiom can be derived from ZF. How do you arrive at conclusions about the ordering? Like everything else in math, by deriving theorems from axioms according to the laws of logic.
* I do not think that a "number" "is" anything. The debates on what is a number is a meta-mathematical debate, not a mathematical one. I know what I mean by "real numbers" (a complete ordered field), and I've seen half-a-dozen proofs that the existence thereof follows from the axioms of ZF to know that it's reasonable to assume it's existence. (I know what I mean by integer numbers, or rational numbers, or other variants). My only argument was that calling the real numbers "numbers" is a matter of convenience among mathematicians. The debates about things like "floating point numbers are not numbers" are superfluous in the strict sense, although they do serve to remind ones that the floating point numbers with the operations as defined by the IEEE standard do not embed in the real numbers, nor indeed in any field. You're free to have an alternative definition of "number", as there is nothing special about the word. Your argument seems to imply that there is something special about the concept of a "number". In math, every definition is merely a matter of convention, and there is never anything special about it.
Um, yes. The real numbers are defined with reference to a limit if you are referring to Cauchy equivalence classes.
There are several errors in the rest of your post. I am going to address this issue first. If we cannot agree on this, there is no sense in continuing this discussion because you are wrong!
I am not quite sure whether your response is to Moshe or to me.
If it is to me, then no, there is no reference to any “limits” in my definition of the real numbers. Neither the definition of Cauchy sequence nor the equivalence relation involves limits. Like I said, there is no sense in talking about limits before you have constructed the reals, because those limits don’t exist.
Actually I am addressing Moshe. How can you say there is no reference to “limits” in the definition of a Cauchy sequence of rational numbers?! Of course there is – the C. sequence is convergent because … it has a “limit”. Convergence implies limit and vice-versa.
You are thinking that convergence means only that the metric d(p_m,p_m+1) = 0 (for all m). This is false. Example: Harmonic series does not converge.
You say there is “..no sense in talking about limits before one constructs the reals..”
For once I agree with you. However, your key problem is that one does use limits to construct the reals according to the definition of a real number using Cauchy equivalence classes. Take the limit away and Cauchy equivalence classes are meaningless.
As I have stated, there is no sense in talking about limit or real number until you have defined one without using the other. Limit is the “idea” of real number.
If you cannot see this, this conversation is pointless.
Alex, please don’t take offense, but I prefer to communicate with one person at a time. Since it was Moshe who made the accusations of my Knols being untrustworthy, I would prefer to complete this conversation with him.
Moshe: The real numbers are defined with reference to “limits”. If you do not see this, it is pointless continuing this discussion.
* How can I say there is no reference to limit in the definition of Cauchy sequence of rational numbers? Easy. Here is the definition: “A sequence of rational numbers q_n is called Cauchy if for every epsilon>0 there is an N such that for every n,m>N, |q_n-q_m|<epsilon". There is no reference to a limit here, and that's how I say it…I am really not sure what your problem is.
* You are correct, merely |q_n-q_(n+1)|<epsilon is not enough. This is why I gave the correct definition above, and not the incorrect definition.
* One does not use limits to construct the reals, no matter how many times you claim so. Again, I refer you to the construction of reals from equivalence classes of Cauchy sequences — there is no reference to a limit there.
* There are many possible definitions of the real numbers. As I've stated, I usually think of the real numbers as "the unique complete ordered field", and the construction of the real numbers (of which there are many, and I can recite at a few that do not reference limits, including quasi-homomorphisms over Z, equivalence classes of rational Cauchy sequences, Dedekind cuts, the finite ring of the ultra-power of the rationals divided by its maximal ideal and the decimal expansion, all of which do not mention limits in their construction) is just a proof that such a field exists — quite beside the central point, as if there was no proof that the real numbers exist, I would be comfortable with taking it as an axiom. Perhaps you have a definition which defines the real numbers with reference to limits. If you do, I'll be happy to see it, and possibly to agree it's valid. It's certainly not the only one, nor, do I suspect, is it a wildly popular way to construct the real numbers. If you claim you have found an invalid way to construct the real numbers, I am happy to take that on faith alone 🙂
I understand you preferring to have one conversation at a time, of course. I will reply to your comment; if you feel like picking up from there at some point – fine, if not – no problem.
**************************
First, a brief response:
Cauchy sequences are not necessarily convergent. Again, let us work with the rational metric space . Look at the sequence
. Look at the sequence  . That is,
. That is,  where
where  stands for the sequence of 0’s of length
stands for the sequence of 0’s of length  . This is a sequence of rational numbers. It is a Cauchy sequence. It does not have a limit. That is, not in
. This is a sequence of rational numbers. It is a Cauchy sequence. It does not have a limit. That is, not in  .
.
So you are right: it does not make sense to try to define the irrational number as the limit of this sequence, before you have formally constructed
as the limit of this sequence, before you have formally constructed  . This limit does not exist. But it is also wrong to call this sequence “convergent”, when working in
. This limit does not exist. But it is also wrong to call this sequence “convergent”, when working in  . Because, again, it does not converge.
. Because, again, it does not converge.
Of course it is true that the “idea” behind the definition of the real number above is a “limit” of the sequence above. But this is just an idea. Perhaps you mean the “idea” of a limit in the world of ideas of Plato. Fine. But this is philosophy, not math. The formal definition can not go through the notion of limit, because it does not exist in . And yes, if you try to define reals like that using limits, you will get something which is not well defined. This is why this is not how this is done in mathematics.
. And yes, if you try to define reals like that using limits, you will get something which is not well defined. This is why this is not how this is done in mathematics.
But just the fact that the definition you have in mind does not work, this does not mean that the reals are not well defined. They are. Using a better definition which I have already described to you.
*********************************
Now, let me elaborate just a bit.
One has to come up with a different definition that does not mention limits. One such definition is a formal construction of a completion of a metric space that I described before. It does not mention limits, just equivalence classes of sequences. You claim that if you take the “idea of limit away”, this construction becomes meaningless. I don’t understand what that means. The idea of a limit is just a motivation for this construction. If you claim that without the motivation, the construction loses its meaning, it is a philosophical statement, not a mathematical one.
The important point that I am trying to get across is the following: one should not call a Cauchy sequence of rational numbers convergent and talk about its limit just because it converges in the completion.
Given a metric space , there is an ultra-power construction (which you may be familiar with) of a metric space
, there is an ultra-power construction (which you may be familiar with) of a metric space  (containing
(containing  ) in which every sequence of elements of
) in which every sequence of elements of  converges.
converges.
Now, would you call every sequence in convergent just because it convergence in the ultra-power
convergent just because it convergence in the ultra-power 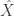 ? I wouldn’t. Just like I wouldn’t say that every Cauchy sequence in
? I wouldn’t. Just like I wouldn’t say that every Cauchy sequence in  converges, just because it converges in the completion.
converges, just because it converges in the completion.
Behind the construction of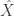 is, again, the “idea” of a limit. It is less intuitive for us to think of an idea of a limit of a sequence like
is, again, the “idea” of a limit. It is less intuitive for us to think of an idea of a limit of a sequence like 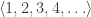 . But sometimes it is convenient to take a compactification of the space you are working with, and force sequences to converge. This is an important idea, an important construction with lots of application. Still, the fact that there is an “idea” of a limit of the sequence
. But sometimes it is convenient to take a compactification of the space you are working with, and force sequences to converge. This is an important idea, an important construction with lots of application. Still, the fact that there is an “idea” of a limit of the sequence 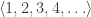 and there is a construction of a metric space which contains
and there is a construction of a metric space which contains  in which this sequence converges, does not make this sequence convergent in
in which this sequence converges, does not make this sequence convergent in  .
.
Same is true for Cauchy sequences. The sequence I described above is Cauchy and does not converge in . The sequence
. The sequence  , on the other hand, is a Cauchy sequence which converges in
, on the other hand, is a Cauchy sequence which converges in  to 0.
to 0.
Constructing is just a formal way of adding limits to all the Cauchy sequences in
is just a formal way of adding limits to all the Cauchy sequences in  . Like I said, there are formal constructions that add limits to sequences which is harder for us to think of as convergent. Behind all this constructions is the idea of a limit. But the formal definition can not use the notion of a limit, because before the construction is completed, these limits do not exist.
. Like I said, there are formal constructions that add limits to sequences which is harder for us to think of as convergent. Behind all this constructions is the idea of a limit. But the formal definition can not use the notion of a limit, because before the construction is completed, these limits do not exist.
Still, all of those constructions (in particular, that of the real numbers) are well well defined.
*****************************************
Finally, a response to just one “criticism” of yours.
It took me some time to parse your sentence
“you think that convergence means only that the metric d(p_m,p_m+1) = 0 (for all m)”
Obviously this can not be what you mean, because d(p_m,p_m+1) = 0 means (by definition of metric) that p_m = p_m+1. So the only sequence satisfying this requirement is constant. Since you are talking about math, please do try to be precise.
Perhaps what you mean is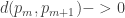 when
when  . So obviously I don’t “think” that. Nor do I think this is enough for the sequence to be Cauchy. If I did think that, it is doubtful that I would have been awarded a PhD in math and allowed to teach math classes at UCLA. You will have to accept the fact that you are talking to mathematicians who know what it means to converge (and don’t “think” it might be something else). And what it means to be a Cauchy sequence. And that these two are not the same (even though given a Cauchy sequence there is an “idea” of it limit, which is formally realized by the completion construction). The example that I gave above shows a non-convergent Cauchy sequence.
. So obviously I don’t “think” that. Nor do I think this is enough for the sequence to be Cauchy. If I did think that, it is doubtful that I would have been awarded a PhD in math and allowed to teach math classes at UCLA. You will have to accept the fact that you are talking to mathematicians who know what it means to converge (and don’t “think” it might be something else). And what it means to be a Cauchy sequence. And that these two are not the same (even though given a Cauchy sequence there is an “idea” of it limit, which is formally realized by the completion construction). The example that I gave above shows a non-convergent Cauchy sequence.
Not so cleverly avoiding my questions and misrepresenting my comments again.
Every Cauchy sequence is equivalent to a convergent sequence for sequences in R. An implication of this statement is that a real number is defined in terms of some limit. And since we cannot agree on this, I am going to stop right here.
Don’t trust anything you find in a knol? Hmmm, I suggest you change your blog to:
Don’t trust anything you find on the web, especially Wikipedia and those who are affiliated with it.
“Every Cauchy sequence is equivalent to a convergent sequence for sequences in R”.
True. But the definition of R can not go through sequences in R. That would be a circular definition, and of course not a good one. It goes through sequences in Q, and for them these notions are not equivalent.
The definition you have in mind of R uses R. That is, it uses the limit points of Cauchy sequences, which exist only in R, but not in Q. This does not make sense. Of course, if this definition were used by mathematicians, you’d be right: the reals would not be well defined. Fortunately, mathematicians use a better definition which works in Q only and does not mention those non-existent limits.
You can continue walking around telling everybody that a circular definition of R that you have in mind does not make sense. This is true. But saying that there is no good definition, which is not circular, is simply false.
P.S. I apologize for continuing a conversation that you have explicitly said you didn’t want to have. Since you have disabled comments on your posts, there is no other forum for me to have this discussion. I do not, however, expect a response (since you have told me you are not interested in responding). I would, if I were you, take other people’s criticism seriously, if you want to be taken seriously by them, but this is entirely up to you, of course.
Alex: One cannot construct the real numbers you talk about without using the concept of limit. Even Cauchy sequences of rationals must have the least upper bound property to define your concept of “real number”. Does this ring a bell for you?
Least upper bound implies …. yes, “limit”. But what is this “limit”. The phrase least upper bound is not well-defined because it implies “real number”.
If you can’t see this, what’s the point in carrying on this discussion?
John, please read this response carefully – it is very short. It seems to me that you ignore a lot of what I say.
“Even Cauchy sequences of rationals must have the least upper bound property to define your concept of “real number”. Does this ring a bell for you?”
Of course it “rings a bell”. But let me repeat what I said before: this is not used in the construction of the real numbers from the rational numbers. The existence of a least upper bound is an axiom in the axiomatic definition of the real numbers. You may say that you do not believe in this axiomatic definition. But this is a different issue.
If the existence of the upper bound were used in the construction of the real numbers from the rational numbers, the construction would be invalid. Here I agree with you.
But the construction that I presented does not use any of this. You start with a definition of a sequence of rational numbers being Cauchy (I believe you give it in your knol article). Giving the definition does not require limits or upper bounds. Then you take the set of all Cauchy sequences. I called it before. The set
before. The set  is defined as a set-theoretic quotient of
is defined as a set-theoretic quotient of  modulo an equivalence relation that I defined in one of my previous comments. Again, no limits or upper bounds are required in either the definition of the equivalence relation or the set-theoretic operation of taking the quotient.
modulo an equivalence relation that I defined in one of my previous comments. Again, no limits or upper bounds are required in either the definition of the equivalence relation or the set-theoretic operation of taking the quotient.
You have never replied to my very simple question: where do you see a problem with this very simple set-theoretic construction? Where do you see limits or upper bounds?
The construction you presented most definitely uses limits. Equivalence classes are determined by the limit (I demonstrate this in my knol called Are the real numbers well-defined?) which is the attribute they have in common. If one writes [pi_1] or [pi_2] or [pi_3], what do you think this means?! It means all these equivalent classes have a common “limit”. You appear to have missed this point entirely.
I read your knol article, but I disagree with your statement. Like I said, I agree that the motivation behind the definition of the equivalence relation comes from a certain idea of a limit. Of course the construction is made to work so that pi_1 equivalent to pi_2 if and only if once you pass to the completion both of them converge to [pi_1] = [pi_2]. But saying this is very different than stating that the construction uses limits. Because the construction makes perfect sense in Q, without passing to the completion.
Let us forget for a second about irrational numbers. Our whole universe is Q. Neither I or you are allowed to talk about anything except rational numbers. Do you agree that for a sequence p_i, being Cauchy is well-defined? You say: for every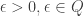 , there is
, there is  such that for
such that for  ,
,  , there is
, there is  such that for
such that for  ,
,  .
.
Both of the definitions use nothing but rational numbers. And don't tell me that this definition is meaningless if you forget about the motivation: like I said, this not a mathematical statement. The argument is whether the equivalence relation uses anything beyond rational numbers, and clearly, it does not.
I give up… I’ll say it without the latex (although clearly you know the definitions. There is some more basic disagreement which I don’t understand).
Cauchy: for every epsilon positive rational there is n such that for i,j>n we have |pi-pj|<epsilon. Similarly for the eq. relation.
again, I’ll need Moshe’s help tp fix the latex code.
Here is what I wanted to say: being Cauchy is well-defined? You say: for every positive rational, there is
positive rational, there is  such that for
such that for  , we have
, we have  , we have
, we have  .
.
I have updated the knol called
Are the real numbers well-defined?
If you scroll down to the end, you shall see the update.
http://knol.google.com/k/are-the-real-numbers-well-defined
This is all I have to say regarding Cauchy and his theory of real numbers. If you don’t see it, I do not know what else to say.
1. I do not run wikipedia, or write for it, or learn mathematics from it. It is possible that there are mistakes in wikipedia (I have seen some myself) or that their definitions are not precise or accurate. This has nothing to do with our discussion.
2. Nor do I care whether Cauchy’s original definitions were wrong. I am a mathematician and not a historian. Although it is interesting to see what Cauchy’s theory of real numbers originally was, I am more interested in the concepts, and not in the history of their development. The fact that Cauchy sequences are called Cauchy does not mean that today mathematicians follow his definitions word by word.
In short, I don’t understand what you are trying to convince me of. If it is that there are mistakes in wikipedia or that Cauchy’s original definitions were wrong, my answer is quite simple: I don’t care. All this is besides the point, as far as I am concerned. Your article claims that the real numbers are not well defined in mathematics. All you are saying is that they are not well defined in wikipedia, and that Cauchy did not give a good definition. This very well may be, so what?
Yes, the quotes you write in your article lead to circular definitions, hence if one were to use them, they would be mistaken. Read the definitions that I gave and you will see that they do not mention real numbers.
If you have constructive criticism concerning what *I* am saying (which is what any reasonable mathematician would tell you), you are welcome to express it. Criticising wikipedea and 19th century mathematicians is not helpful.
Your only criticism of the definition on wikipedia is that they say “for every positive real epsilon”. Sure, it should be for every positive rational number epsilon, like in my definition above. A very minor change in the definition, which you could have easily thought of, instead of writing a whole knol article about it.
This gives you a good definition of Cauchy sequences and a good definition of the equivalence relation on them. Hence a good definition of R.
If you have indeed come up with another construction of R, provided that it is correct, an article about it would actually be interesting. But it seems that your article is just based around the fact that the definition on wikipedia requires a small modification…
I refer to Wikipedia because that is where most others get their information. I also do not care what is written there. I think for myself.
If you replace Wikipedia’s definition with “for every rational number epsilon”, it would be untrue.
Can you find a rational epsilon in any case for any irrational number? The answer is no.
One last comment: your article seems to suggest that this definition is the only known definition of the real numbers, and if it falls, the whole theory of real analysis falls. This is also not accurate. There are several definitions of the real numbers, and only on of them mentions Cauchy sequences. Possibly you are unaware of them, but if you are really interested in the subject, maybe it is a good idea to look a bit in the literature. And by this I do not mean wikipedia.
All of those definitions, including the one with Cauchy sequences (the way I gave it) are good (and equivalent, of course). Again, if you can give another construction (which, if is correct, will be equivalent to the other ones), this is, of course, of interest.
Alex: None of the constructions of the real numbers I have seen convince me and I have seen several. The two main constructions are:
1) Convergent sequences of rational numbers
2) Dedekind cuts
You are correct that I do not cover all the constructions in my knol – that was not its purpose. I covered only the main construction – by Cauchy sequences. Did you read my knol called “Exactly what is an irrational number?” It gives the astute reader a clue as to how I would construct the real numbers.
Unfortunately it will have to wait until I publish my book called:
“What you had to know in Mathematics but your educators could not tell you.”
I cannot agree with you that either of the above constructions are valid and see no point in debating this. Unlike you, I am not a product of any university even though I have completed all these advanced courses at “brick and mortar” (not online) universities.
John,
Actually, replacing “for every real positive epsilon” with “for every rational positive epsilon” is the definition that works. In fact, it is enough to restrict yourself to (for example)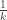 for every natural number
for every natural number  .
.
What one is trying to capture in the definition of a Cauchy sequence is that (which is itself a positive rational number – not that it matters very much) is getting arbitrarily close to 0, so you might as well define it with
(which is itself a positive rational number – not that it matters very much) is getting arbitrarily close to 0, so you might as well define it with 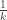 for every
for every  (or any other sequence of rational numbers that converges to 0). The precise definition would be:
(or any other sequence of rational numbers that converges to 0). The precise definition would be:
A sequence of rational numbers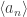 is called Cauchy if for every natural number
is called Cauchy if for every natural number  there is a natural number
there is a natural number  such that if
such that if  , then
, then  .
.
As you see, everything only uses rational numbers (of a very simply form).
The equivalence relation on Cauchy sequences is defined similarly. Those definitions are equivalent to the ones with "every positive rational epsilon".
For the other constructions of the real numbers that I had in mind, I can currently think of two:
1. A purely algebraic one, that has to do with a real closure of a field.
2. A construction that goes through nonstandard models (which is basically purely algebraic, but also uses the Compactness Theorem in Logic): one takes a nonstandard ordered field, takes the ring of finite elements and divides it by the ideal of the infinitesimals.
I will read the knol article you have mentioned (“Exactly what is an irrational number?”). I am interested to see the ideas behind the construction that you propose.
Just a note here — one beautiful construction of the real numbers, using nothing more than functions from integers to integers, is described in http://www.maths.mq.edu.au/~street/reals.pdf (in the interest of completeness, I got the link off of Wikipedia). This construction, beyond its elegance, has the advantage of having been formally verified — please see http://isarmathlib.org/Real_ZF.html — this is about as formal you can possibly get, with a computer checking the proof for errors.
Alex,
All fair and well, but k is a natural number. Neither k nor its reciprocal 1/k define a “real number”.
Furthermore, this k is not unique, so what does it tell one about a particular “real number”?
All fair and well, but k is a natural number. Neither k nor its reciprocal 1/k define a “real number”.
True. This only defines a Cauchy sequence. My only point was that this definition of a Cauchy sequence (unlike the one on wikipedia, and possibly the one that Cauchy originally gave) is good (that is, it only uses rational numbers). BTW, note that most of Cauchy sequences like this do not converge (in Q).
Now that we have a good definition of a Cauchy sequence of rational numbers, let be the set of all Cauchy sequences (according to this definition). Now define the equivalence relation
be the set of all Cauchy sequences (according to this definition). Now define the equivalence relation  that I proposed:
that I proposed:
Given two Cauchy sequences , define
, define  if for every natural number
if for every natural number  there is a natural number
there is a natural number  such that whenever
such that whenever  , we have
, we have  .
.
Again, all we are saying is that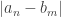 , which is a non-negative rational number, comes arbitrarily close to 0 when
, which is a non-negative rational number, comes arbitrarily close to 0 when 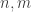 go to
go to  . So it is perfectly fine to define this with
. So it is perfectly fine to define this with 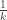 for all
for all  . Again, this definition is good (uses only rational numbers).
. Again, this definition is good (uses only rational numbers).
Now the set of real numbers is the set-theoretic quotient of modulo
modulo  . So a real number is an equivalence class of
. So a real number is an equivalence class of  modulo
modulo  .
.
As you can see, all steps of this definition use only rational numbers.
Rational numbers can be identified with those equivalence classes which contain a constant sequence. So a real number (an equivalence class as above) is rational if and only if it contains a constant sequence. It is easy to show that this is equivalent to: all sequences in that equivalence class converge in Q.
This is still not well-defined. You say a real number is defined as the equivalence class of B mod E. But how is B mod E defined?
I know where you are leading but am playing your game to show you that Cauchy’s theory does not define a real number, not even close. If B mod E is defined the way I think it is, then you still have an ill-defined definition of real number.
Alright: this is a general set-theoretic definition.
Let B be any set, and E be any equivalence relation on B.
Lemma: There is a unique partition of B into disjoint subsets such that: 1) If C is a set in this partition then for every a,b in C, we have E(a,b), and 2) If C,D are two different sets in this partition, a in C and b in D, then not E(a,b).
These subsets are called equivalence classes. Now B/E is simply the collection of all the equivalence classes.
If you don’t believe the lemma, I can sketch the proof. If you do, I hope you agree that the definition of B/E is good.
In our particular case: B is the set of all Cauchy sequences. Two sequences are equivalent if they come “as close as possible” (I defined it formally before). One equivalence class is a collection of sequences such that any two of them are equivalent (and if you take two sequences from different equivalence classes, they are not equivalent). R = B/E is the collection of all the equivalence classes. So a real number is defined as an equivalence class like that. In other words, a real number is (by definition) a set of equivalent Cauchy sequences.
Side remark: I saw you speak about groups in your knol article. The general construction above is a set-theoretic generalization of the group-theoretic quotient, which, I am sure, you are familiar with. For example, if G is a group and K is a subgroup, then one defines the group theoretic quotient G/K (I am sure you know the definition. If K is normal in G, then G/K is also a group). This is just a special case of the set-theoretic quotient I defined above. In this particular case, the equivalence relation E on K is defined as follows: E(a,b) if and only if ab^{-1} in K.
I expected this response. Now for the sake of those who know nothing about groups or set theory, to speak of equivalent Cauchy sequences (real numbers) means that one can show a) their partial sums have the *same* least upper bound. b) one can derive a sequence from an equivalent sequence in a finite number of operations if the sequences are indeed equivalent.
a) is the definition of a real number in terms of a least upper bound or *limit*.
b) demonstrates the sequences are equivalent but says *nothing* about a real number.
So again, the defining attribute of equivalent Cauchy sequences of rational numbers is the *limit*.
Since we are working in Q, partial sums of a Cauchy sequence, which does not converge in Q, do not have a least upper bound. This “limit” does not exist, and I do not talk about it in my definitions. The definition is precisely what it is: an equivalence class of Cauchy sequences (and no limits or least upper bounds are required in order to give it, just basic set theory).
In your knol article you criticized the definition on wikipedia because they use a real epsilon in order to define real numbers. I agreed with you and gave you an alternative definition that does not use real numbers. From what you are saying in (b), it seems that you do not have any mathematical criticism, but rather a philosophical one (” … but says *nothing* about a real number”). This does not mean that real numbers are not well defined in mathematics.
If your article were called “why I don’t like the definition of real numbers using Cauchy sequences”, I would not be arguing with you, and if you explained your point (b) in detail, I would be interested in understanding what you mean. But saying that there is no good (that is, mathematically correct) definition of real numbers using Cauchy sequences is simply not true. So far I have taken care of your only mathematical criticism, and you haven’t produced any new one yet.
Well, if this limit does not exist as you say, then I say, that whatever you are defining can be called anything you like. For example, you can call such equivalence classes “Alex”. And this tells one nothing about a real number.
Every real number that is not rational contains an irrational part that is incommensurate. Now, if such a part cannot be measured and the Cauchy definition deals solely with partial sums, it is discarding an irrational part (if it is an irrational number one is considering). Let a real number k = r + ji where r is the partial sums from your Cauchy sequence and ji is some multiple of the successor of zero (soz). The soz of course cannot be defined theoretically but one assumes there are no holes in the real number line. Therefore, soz exists in reality but not in theory.
The Cauchy definition completely disregards soz and the fact that a limit cannot be computed in its “finality” for any real number. Well, the limit is always some value that academics attribute to r in my definition above for the real number k.
Since neither r nor i can be fixed, it (the limit of k as the partial sums of r) does not exist. This means one always thinks of real numbers as approximations which is why they are not well-defined.
Let us suppose the successor of zero exists. Mind if I call it s? Anyway in any case either s is rational or s is not rational. As the successor of zero there exists no number r, such that 0 < r < s.
Case 1: S is rational. From implication of successor (to be after) we have s is positive. We take s/2. s/2 is in Q, since Q is closed under multiplication. Since s is positive 0 < s/2. Also, s/2 < s. Thus 0 < s/2 < s. However, this contradicts s as the successor of zero. Thus, the successor of zero does not exist.*
Case 2: By a similar argument replace words rational with irrational and symbols Q with R.
As both cases imply a contradiction we can say there is no successor of zero.
*Note it would suffice to in case one say s is not rational and in case two s is not irrational.
Um no. S cannot be rational so your reasoning is faulty. Now since irrationals are not well-defined, you cannot just replace Q with R.
John, I used a logical tautology, P or ~P. You cannot say it is incorrect. Like saying I am either male or not male, just because I am not male makes no difference, the statement is true.
None the less, I have mistaken used properties of real numbers. We shall use your defintion any q in R is defined as r + js, where r,j in Q, s in Q’. Yes? Hence, like Complex numbers are RxR[i], your number system is what? QxQ'[s]? QxQ[s]?
Thus, this should be closed under addition and multiplication and as j in Q.
If what I have said is true, tell me what happens if using (r,j) notation I take the point (0,1/2)?
I can say it is incorrect, because it is. You cannot use knowledge of rationals to prove a result on a concept that is not a rational. Then, you cannot assume that if it’s not Q, it must be ~Q. It can be neither. Furthermore, P or ~P is not a tautology. Tautology means a needless repetition. You are not using it correctly. Do you normally use needless repetitions to extend your theories to new concepts that may not have any relation to existing theory? Sounds absurd to me.
The successor of zero is neither rational nor irrational. For one thing, “irrational” is not well-defined.
Also you need to be very careful when you extend theory: Just because something is true in Y, does not automatically follow it is true in X.
I am not interested in continuing this dialogue. I know I am correct (and most mathematicians are incorrect). Unfortunately I do not have the time to respond to every comment. Please don’t interpret this as being ignored by me.
Tautology: in logic means a statement which is always true. Hence, John you are incorrect. However, you are right my proof is wrong as it requires s to be “real”. Hence I apologize. However, I believe I have intepretted you correctly in my second post. That is G* = QxQ[s], much like C = RxR[i]. *Where G is the Gabriel definition of the Reals.
Thus, you have to at this point answer the following questsions. First, is G = QxQ[s]? If so, you arrive at a contradiction given (0,1/2). Do you mean QxN[s]? However, that construction requires rational numbers to have a rational successor, i.e. between rational p,q there exists no other rational. This is not true. Second, are what I deem irrational constructible in this construction? (Like pi) Third, how do limits work? is Lim of pi/n as n goes to infinity 0 or s? If you do not like limits, then tell me if I am to select an arbitrarily large number and small one what is the ratio, 0 or s? Finally, if you can answer those can R = G? The finite cross-product of countable sets is countable. Thus, you need a proof R is countable aside from John Gabriel claims Cantor’s proof is wrong. If this is true, then I can claim John Gabriel’s proof is wrong… which is incorrect because I haven’t proved anything with that claim.
You are not interested in continuing because you are correct? If I had a radical idea that would change the world I would come up with the most rigorous proof and rub it in there face. If someone questioned me before it was done I would show them the skeleton proof and say find the error. If they proved me wrong like what happens when you consider my above questions, I would try to see if I could make it work, if not time for a new theory.
QED baby \puts on sunglasses
Main Entry: tau·tol·o·gy
Pronunciation: \tȯ-ˈtä-lə-jē\
Function: noun
Inflected Form(s): plural tau·tol·o·gies
Etymology: Late Latin tautologia, from Greek, from tautologos
Date: 1574
1 a : needless repetition of an idea, statement, or word b : an instance of tautology
2 : a tautologous statement
To say P or ~P is a not a tautology. What if neither applies? As you admitted, s in your argument is required to be real, therefore any statement P or ~P is irrelevant, yeah?
Sigh.
Oh nice definition. Using MW Dictionary we look up “tautologous statement”
Main Entry: tau·tol·o·gous
Pronunciation: \tȯ-ˈtä-lə-gəs\
Function: adjective
Etymology: Greek tautologos, from taut- + legein to say — more at legend
Date: 1714
1 : involving or containing rhetorical tautology : redundant
2 : true by virtue of its logical form alone
— tau·tol·o·gous·ly adverb
Oh, I’m sorry, does that say true by virtue of its logical form alone?
Again, the reason I claim P or ~P to be wrong has nothing to do with the proof, rather your claim on the number. I mistakenly assumed you would use a “real number” to describe the reals, instead of whatever s is.
Again, nice to dodge the questions which contradict your definition.
Let us again consider x = r +js notation. Does it follow additive properties. It does. Thus we have the succesive set: {-s,0,s}. So I want to consider the open topological neighbor around 0, N(0,s)… or closed neighborhood? Thus this system does not follow Euclidean or square metrics.
Does it follow multiplication?
It has to have a multiplicative inverse right? So what is 1/s? Is this infinity?
Given: x = r+js, y = q + is, z = p + ks.
What is xy? (r+js)(q+is)? rq + (j+i)s + ijs^2?? What is s^2? Given 0 < s < 1, then s^2 < s… but x^2 \geq 0. So s^2 = 0? Thus any multiplication of two irrational numbers is rational?
Or is it rq + (j+i+ijs)s? But then (j+i+ijs) is not in Q…
Or does the multiple not have to be in Q? Then by making the multiple m/s, m in Q, you have infinite ways to represent each rational!
Ahhh, you might say s^2=s!
Lemma s^2 s
Assume s^2 = s
Then x^2 – x = 0 has 3 solutions
Since, x(x-1) = 0
-><-
Thus s^2 s!
Given this do you still believe your definition to be correct? You only have one binary operation, which forces your space to fail the metric meausures of Euclid and Square or any derivation from the two. Given this are you satisified with the space you described?
x = r + js is not my deinition. This is how most acedemics define a real number. They then proceed to discard the successor of zero and define the real number to be a “limit” of the partial sums of r.
Tautology is a Greek word. Did I mention I speak Greek? Tauto pronounced tafto and logy pronounced loyia means something that is self-identifiable.
P and ~P are a tautology if and only if the statement you are considering is P. However, as you admitted, s is not a real number.
Notice I said let a real number k = r + ji. I was only using this to illustrate that the concept of limit is based on this and thus ill-defined.
So in trying to prove the defintion you erroneously think is mine, you are harming your argument. Try to read more carefully is all I can say. Good luck!
Nonetheless, x = r + js is only used by John Gabriel. Or “Let a real number k = r + ji where r is the partial sums from your Cauchy sequence and ji is some multiple of the successor of zero (soz). The soz of course cannot be defined theoretically but one assumes there are no holes in the real number line. Therefore, soz exists in reality but not in theory.”
did I perhaps miss quote you? (“where r is the partial sums from your Cauchy sequence”)
Thank you for giving me the etymology of a word that I can get from the Oxford dictionary. Your ability to speak Greek has no bearing, likewise my ability to speak French. If by chance you were implying that because you speak Greek you are like the Greek mathematicians of old, I will say perhaps or perhaps not. However, I will say the ability to speak French is a requirement for a doctorate in math (or Russian) as you have to translate into the foreign text.
However, if I were to say 5 is either blue or not blue, this is a tautogoly. Although 5 is not a colour, only can clearly see 5 is either blue or 5 is not blue. However, I said my argument was wrong because you will not believe any proof with real numbers.
However, I have also shown given the properties you wish s to have, you will not have a valid number system.
Regards,
Although I use the example x= r + js, there is nothing unusual about it and it is not my definition as you claim. If you don’t like the js part, you can discard it and you have your definition of real number, that is, some real number r that you claim to understand by use of Cauchy’s theories.
I do not construct the real numbers using x=r+js because this implies one can do arithmetic with s, which as you noted is clearly false.
“If I had a radical idea that would change the world I would come up with the most rigorous proof and rub it in their face.”
Did I quote you correctly? Well, I don’t consider my ideas radical by any stretch of the imagination. Also, do you think it might be a tad presumptious of you to think that I would do what you suggested? This is called projection – I would have thought someone like you avoids this type of thinking, being of collegiate character and breeding you claim to be.
If you read my comments carefully, I stated that I intend to publish this construction in a book which I plan to sell for profit. Sorry, this is all I can say regarding this matter.
In the meantime, Moshe has not responded to my last comment.
John,
I would like to apologize, I had mistakenly believed that given x = r +js you meant x to be defined as the real numbers. As such, for this misunderstanding I do wish to apologize.
However, the concept s, does not exist in reality. Since theory is used to describe reality and it does not exist in theory.
You say concept of real numbers. If you don’t like radix might I suggest adic or continued fraction numbers for further study?
Personally, I have taken aliking to adic numbers over my study of them. Adic’s have the property that using no decimals they create a number system equal to (in cardinality) the reals and greater than the integers. This is why any wish you may have to make the reals countable is unimagineable, I think is the right way to say this.
So do as you may, but I would suggest picking up a Topology book (I happened to like my reading of Munkres) to gain an abstract conception of sets, and any number theory book with adics included.
You may scoff, but I believe your concept of infinity is the crux to seeing things. Having read some of your knols you have done some calculus without limits although there is an extending condition on your calculus in some cases where continuty or “from the side of” are needed where limits disregard this and have simpler assumptions. However, they were still a decent read.
However, Final Question… What is the cardinality of the collection of subsets of the natural numbers? Clearly it is infinite. Thus, if you believe this to be aleph, can you find the surjection from N => P(N)?
(You do not need to provide an injection since I can provide injective g:N => P(N), given g(n) = {n})
I know all the theory and think I understand it. I just don’t agree with all of it. Not saying it is all wrong, but it has serious problems.
Let’s say I have an issue with “infinity” being a cardinal number or any number as for that matter.
infinity is not a number in many number systems just a concept. However, from the continuum hypothesis we know |N| = aleph naught, but is uncertain to determine whether the reals (where |R| = beth naught) are an aleph, and if so impossible to prove which aleph, all we know is they are not aleph naught. Many, myself included, believe |R| = P(N) = aleph one. This is well, the more soothing of the possibilities, considering |R| > aleph one quickly leads to infinitely many infinite sets between the N and the R.
A quick sketch of that proof is like given two rational numbers how many are inbetween.
This line clears up my confusion: “I know all the theory and think I understand it. I just don’t agree with all of it. Not saying it is all wrong, but it has serious problems.”
This is to say our problem now lies in the fact that you reject certain mathematical axioms. Since the axioms imply the theories.
As for your problem with infinity as a number, it really is just a concept. Think of it this way: You walk up to two people the first says, “1,2,3,4…” when asked what he is doing he says counting to infinity. This is perfectly acceptible as we know what he is doing is valid. Now the second says, “…,-4,-3,-2,-1”, and exclaims he counted up from negative infinity. This claim is absurd is it not?
However, in inverse geometry, another one of my favourite areas, infinity is cleverly solved. Also, projective planes use infinity as a point.
Does what I say make sense?
This is why it is impossible to surject the naturals onto the reals, since even {0,1}^N is uncountable.
Correct. It took you a long while to realize this, that is, the fact that I reject Cantor and all his absurd ideas. Better late than never.
I demonstrated the naturals can be placed into a one-to-one correspondence with the real numbers in the interval [0,1].
But I think this was not the reason Moshe set up his web page – rather it was to discredit my opinion of Cantor – the father of mathematical cranks.
Projective geometry: If paths of different lengths contain a different number of points, then it is possible to show in certain cases that real intervals can be mapped onto other real intervals of different lengths. Yes, you read this correctly: a mapping of reals onto reals. Do you know how? If you did, you would seriously doubt Cantor’s theories of greater infinities.
For anyone to say infinity is cleverly solved , does not say much about one’s intelligence except that it (one’s intelligence) can be doubted.
John, you misread my statement: “However, in inverse geometry, another one of my favourite areas, infinity is cleverly solved. Also, projective planes use infinity as a point.”
I refer to inverse geometry for cleverness, please comment on this area if you think it to not be clever.
In addition, I guess I should further explain I mean projective planes are formed from taking the parallel classes of an affine plane and adjoining them to a point at infinity. Again, I apologize for not making this clear. Although, all projective lines are equally long so I do not understand the statement: “If paths of different lengths contain a different number of points.” Finally, I do not find it hard to believe the real interval [a,b] can be mapped to [c,d]. In fact I believe the simplest map is the line through points (a,c),(b,d).
Finally, let us for a moment consider the following thought experiment. We note the vector {0,1}. I define the infinite cross product to be (for example finite {0,1}X{0,1} yields, {0,0},{0,1},{1,0},{1,1}) the designation for which naturals ({1,…,n,…}) are in the subset of. Hence Null = {0,0,0……}, 0 = {1,0,0,….} {0,1} = {1,1,0,…} and hence forth, such that if a natural number n is in the subset the nth term is one, if it is not the nth term is 0.
Claim: Given a bijection from N to an infinite collection vectors, there exists a subset of N not described by these vectors, and hence there exists a vector not described by this bijection. Hence, there exists more vectors than natural numbers.
Claim: There exists as many vectors as Real Numbers on the interval [0,1).
Which claim if either do you believe I am unable to prove?
I believe you misread my statement. Let me simplify it for you: infinity is not a problem so that it can be solved.
Ah, but if I wish to define 1/0 is there a problem? Inverse geometry gives me a definition of r/0. This I believe to be cool…
Please, your knol claims you wish for a new proof the Reals have no bijection to the naturals. Thus, I am merely presenting an argument which disproves there exists only one infinity. (This is an issue that many of my philosophy professors had, it is a rather disturbing claim.) From this it should easily follow the reals are larger. Again, there are two steps I skip over from claim one to claim two, but because they are unrelated to axioms. The first requires axiom of infinity and perhaps countable choice. The Second does not require axiom of choice or continuum hypothesis, however, the use of such proves |R| = 2^|N|.
Actually it proves |R| = aleph_one
You are a hopeless case as I suspected.
Strong claim. Perhaps then you care to comment on my contruction. Obviously, the claims I can prove, I am merely asking if your intuition can see they are true.
On Jan 6th, 2009, the following appeared in one of my comments to you:
“I am not interested in continuing this dialogue. I know I am correct (and most mathematicians are incorrect). Unfortunately I do not have the time to respond to every comment. Please don’t interpret this as being ignored by me.”
This web page was set up by Moshe to warn readers about my claims regarding the real numbers being well-defined. Alex took over after Moshe abdicated his role. Now Alex has abdicated and I do not care to discuss Cantor’s useless theories. You can read what I have to say in my knol called Are the real numbers uncountable?
And your idea is wrong, my two claims not only show there exists more than one infinity they make the real numbers well defined iff they are well defined on the base 2 interval [0,1] which is iff the power set of the naturals is well defined which is iff the naturals are well defined…
I would read your book if it were published with the subtitle a theory by John Gabriel with no mathematical basis, because as so far any mathematical disproof of your ideas is not “well-defined” However re-read my claims, the proofs are simple you should be able to come up with them, they are both combinatorial proofs, for rigour I suppose actually definitions could be used but simply put I wrote these to be counting proofs so it requires only intuition. The point in being so you comprehend there exists different kinds of infinity.
Hahaha, looking at it my construction really is bizarre, and maybe not intuitive. Sorry. Wonder if it really works….
Hmmm, let x in [0,1] be a random string of digits base 2. Yah it works… no x I can’t hit! woohoooo!
If you can prove a surjection from N => P(N) your ideas are valid.
My proof provides a surjection. If real numbers are treated as approximations (which they really are), my proof provides a bijection.
If you accept that all real numbers can be represented in base 10, then the real interval [0,1] is countably infinite according to Cantor’s definition.
Link follows:
http://knol.google.com/k/are-real-numbers-uncountable#
Ah, mon ami, P(N) has strictly greater cardinality. 2^countable is uncountable, then what is 10^countable? Mon ami, clearly you cannot claim you have all R if you only use finite expansions. Niet, incorrect, wrong, invalid. You claim cantor’s proof is a wrong proof by contradiction? Yet consider my claim: “Claim: Given a bijection from N to an infinite collection vectors, there exists a subset of N not described by these vectors, and hence there exists a vector not described by this bijection. Hence, there exists more vectors than natural numbers.”
This is the same as cantors. We line up an infinite number of reals with the naturals, should we find another the set is uncountable, since we can find one given any permutation of the bijection.
“Mon ami, clearly you cannot claim you have all R if you only use finite expansions.”
Do not address me as “mon ami”.
Who is using only finite expansions? Can you read English properly? The proof uses infinite expansions. My, but you are dim, aren’t you?
“Due to the fact that most real numbers cannot be finitely represented in any radix system, it becomes necessary to make a couple of modifications without any loss of generality:
1) Real numbers in the interval [0,1] are treated as approximations”
So, because you can come really really close to a number means you map to it? So what would 1/3 be? Let’s just say you go 100 digits. What then? What would three times that be 100 digits of 9. That wouldn’t be one…
Anyhow, you still apparently ignore my construction which probably means you cannot find the flaw in it…
Did you read the section that came before this one or do you just like quoting out of context?
The section you are referring to shows how one can form a bijection immediately. The previous section performs the same steps as Cantor’s rational argument. It includes all non-terminating and non-repeating decimals in left-right infinite traversals. In case you missed it, this means 1/3 is included.
http://knol.google.com/k/are-real-numbers-uncountable#
I ignore your construction because it has no relevance.
By of no relevance, I’m going to assume you mean it completely contradicts my ideas therefore I reject it.
So the proof goes continuing from the givens.
Proof of claim one:
We know the naturals are infinite. From the power set of the naturals containing the naturals, we know the power set of the naturals is infinite. We shall take an infinite set of these vectors and create a bijection with the naturals. We now assume this bijection covers all of the power set, and thus there would only exist one infinity. (Here lies the point where you think Cantor’s proof is wrong) We shall now take a simple combinatorial approach. Given the bijection of the naturals to these vector, we can imagine having pictures of these vectors. Now we shall attempt to create a new picture (vector). Thus, we shall look at the nth picture (vector) and note whether the nth term is in or not in the picture (vector). If the nth term is in the picture we do not include it in our new picture (vector) and if it is not in we do. After forming our new picture (vector), we note this picture (vector) is different from every other picture (vector). Hence, this picture (vector) is not in the bijection. However, we know it exists since we just created it. Therefore, this picture (vector) is one of the subsets of the Power set of the naturals. We now note, it does not matter which of the vectors are included, and this can be done under any permutation of given vectors. Therefore, the Power Set of the naturals has a higher infinity than the naturals by contradiction of the assumption.
To get the Map to the Reals, the easiest is P(N) => 2-adics => R.
Else one can use P(N) => [0..1] base 2 => R.
Since many cannot do the first, we simply construct the second, which creates the first bijection by removing commas and braces, and placing a decimal at the left. The second bijection is from base conversion and tangent composition.
By “of no relevance”, I mean no relevance. Nothing else.
You are not a native English speaker, are you? Yes, it’s easy to tell. Your grammar is shocking. It is hard to follow your thoughts. However, I think I understand what you are trying to accomplish.
Unfortunately your conclusion is incorrect. But I shall try to help you out a bit. Start your argument as follows:
“Given the bijection between the naturals and the elements of the power set, it is not difficult to choose an nth set.”
Now continue your argument and remember that when you think of a ‘vector’, you are really thinking of an element of your power set, which by the way is a set. To simplify your argument, just use the nth set and then take it from there.
Once we get your grammar corrected, then we shall focus on your logic. Do you have a last name Michael? Please tell me a little bit about yourself: where you live, what you keep yourself busy with and most importantly why don’t you just go to Moshe and ask him to help you?
Note the vector {0,1}. I define the infinite cross product to be (for example finite {0,1}X{0,1} yields, {0,0},{0,1},{1,0},{1,1}) the designation for which naturals ({1,…,n,…}) are “in the subset of”. Hence Null = {0,0,0……}, 0 = {1,0,0,….}, {0,1} = {1,1,0,…} and hence forth, such that if a natural number n is in the subset the nth term is one, if it is not the nth term is 0.
Claim: Given a bijection from N to an infinite collection vectors, there exists a subset of N not described by these vectors, and hence there exists a vector not described by this bijection. Hence, there exist more vectors than natural numbers.
Proof: For labeling purposes whenever we denote a vector, it shall be understood to be the subset of naturals it is associated with, like in the given definition. Since the naturals are infinite, and contained with the Power Set of naturals, there exists an infinite number of subsets of the Power Set. Hence, there exists an infinite number of vectors. Hence, we shall take an infinite number of these vectors and create a bijection with the naturals. We shall prove by contradiction and assume this bijection covers every vector. Now given the vectors we perform a byte switch at the nth position in the nth vector. Thus, if the nth term is 0 we make it 1 and vice-versa. We note this vector cannot be in the bijection since it cannot be any f(n) as we performed a byte switch at the nth position. Hence, the cardinality of the Power Set of naturals is greater than the naturals by contradiction.
I believe the point of your question to be am i a mathematician? Short answer: yes, Long answer: not really, I am a problem solver who happens to enjoy the areas of Number Theory, Topology, Geometry, and Combinatorics. My proof writing is mainly sketches that encompass the crux ideas. I dislike rigorous proving although, when need be I do write.
To the main point, my name? The doctor perhaps… Hobbies? fun! Reason for continuing? Well I found a lamp proclaiming to be the sun…
When one is not a good writer (I am the first to admit that I am not a good writer), one should avoid using long sentences.
Let’s begin with your first paragraph:
You don’t have to say “Note the vector {0,1}”. All mathematicians know what a vector is. Well, they have a reasonable idea at any rate. If you want more people to understand, then you should use words like set instead of vector, seeing that direction plays no role in your argument.
The next sentence is very poor:
Define the infinite cross product to be x are “in the subset of”.
Why? Well, you have not yet defined what your set will be. The logical way, is to state how your set or sets are defined before you begin to talk about subsets.
Once you have defined the sets and shown some sample mappings, then you can proceed with your main argument.
I have never thought of myself as a ‘lamp’ or the ‘sun’. If this a genuine compliment, I thank you.
I am not going to post here again. If you want me to help you, continue to correspond at john underscore gabriel at yahoo dot com. Also place in your subject line: I have a proof!
Be patient, I receive a lot of emails from readers claiming to have proved the real numbers are uncountable.
When one is not a good writer (I am the first to admit that I am not a good writer), one should avoid using long sentences.
Let’s begin with your first paragraph:
You don’t have to say “Note the vector {0,1}”. All mathematicians know what a vector is. Well, they have a reasonable idea at any rate. If you want more people to understand, then you should use words like set instead of vector, seeing that direction plays no role in your argument.
The next sentence is very poor:
Define the infinite cross product to be x are “in the subset of”.
Why? Well, you have not yet defined what your set will be. The logical way, is to state how your set or sets are defined before you begin to talk about subsets.
Once you have defined the sets and shown some sample mappings, then you can proceed with your main argument.
I have never thought of myself as a ‘lamp’ or the ‘sun’. If this a genuine compliment, I thank you.
I am not going to post here again. If you want me to help you, continue to correspond at john underscore gabriel at yahoo dot com. Also place in your subject line: I have a proof!
Be patient, I receive a lot of emails from readers claiming to have proved the real numbers are uncountable.
Strange……you talk just like moshe rubin
All Cantor’s Delusions (and much more) exposed here:
http://www.spacetimeandtheuniverse.com/math/4507-0-999-equal-one-556.html#post27247
Don’t click on any links provided by “John Gabriel” or any of the “Anonymous” IDs. They contain malware.
What a baboon you are – every one knows that is untrue. Silverstein is not your real name.
Watch many of my YT videos here:
https://www.youtube.com/channel/UClBbBVLs3M-d3dNgU4Vop_A
See especially the 3-PART series entitled Academic Ignorance and Stupidity.
Neither Dedekind Cuts nor equivalent classes of Cauchy sequences are valid constructions of the mythological object known as “real number”: